Poker : MTT et ICM #4 - Perf Tuning avec du Deep Learning

Rappelons-nous une des conclusion du dernier épisode :

(…) le calcul prend 27ms pour une moyenne sur 15500 échantillons. C’est très raisonnable en soi, mais si j’envisage de simuler quelques milliers de tournois comportant des milliers de mains elles-mêmes incluant plusieurs calculs d’ICM, ce ne sera pas suffisant. Damned.

Du coup©™ peut-on obtenir des valeurs tout aussi satisfaisantes mais beaucoup plus rapidement ?

Pour ceux qui nous rejoignent seulement, je vous conseille de parcourir les articles précédents :

• #1 : La problématique exposée sur les fonctions d’évaluation en tournoi de poker
• #2 : L’implémentation d’un calcul exact de l’ICM
• #3 : Un calcul pour un plus grand nombre de joeurs par la méthode de Monte-Carlo

Neural-Networks—Deep—Machine-Learning-Artificial-Intelligence-MotherF****r

Quelques définitions au doigt mouillé :

• le machine learning c’est l’approche pour laquelle la machine n’a pas été programmée pour résoudre un problème explicitement (ce n’est donc pas une heuristique). Elle apprend à le résoudre.
• les réseaux de neurones sont une technique antique (ils datent de 1943) qui convient particulièrement bien au machine learning. On n’a juste pas pu les exploiter pleinement jusqu’à récemment, lorsque les machines ont commencer à envoyer suffisamment de pâté (le fameux point Pâté Hénaff pour nos amis franglophones).

Une minute de silence pour cette vanne, merci.

• les réseaux de neurones ont une couche de neurones d’entrée qui acceptent un signal (des données) et une couche de neurones de sortie qui donne un résultat associé à ce signal. Entre les deux, on peut avoir plusieurs autres couches de neurones, auquel cas le réseau devient profond. Et on commence à parler de deep learning. Ce que permet le deep learning c’est surtout d’extraire des caractéristiques des données d’entrée brutes grâce au seul bourrinage d’un nombre gigantesque de données, au lieu d’essayer de traiter les données en amont pour les rendres assimilables par un réseau de neurones plus modeste, et ce n’est pas rien.

Tout ceci est une sous-partie du domaine de l’intelligence artificielle qui consiste à coder disons… des trucs un peu compliqués. Ici on se fiche un peu de ces distinctions, on va utiliser un réseau de neurones pour faire un calcul qui comprend des additions et des multiplications, et non pas des trucs révolutionnaires qui changent la société comme faire chanter nos dictateurs favoris.

Objectif et paramètres

Depuis la dernière fois, on sait générer des valeurs d’ICM pour une cinquantaine de joueurs avec une précision et une probabilité abitraires. Cependant s’assurer de cette précision probable a un coût. Comme je le proposais précédemment, on peut simplement observer le nombre de tirages nécessaires pour l’atteindre sur pas mal de cas, prendre le maximum, et on ne sera pas bien loin de la garantie initiale pour des valeurs similaires.

On peut donc se dédouaner des checks coûteux de convergence, mais ce qu’on voudrait vraiment pour le solstice c’est un temps de calcul bien plus faible. Genre maximum une milliseconde.

Alors pour ça on va fixer quelques paramètres, parce que si je m’intéresse à 10, 50 ou 1000 joueurs c’est pas le même topo. De même, si seul le premier du classement est payé ou si la distribution des prix est exponentielle, c’est pas bien pareil. Et enfin si tous les joueurs ont le même stack ça diffère franchement de la situation où on a quelques Bezos et des dizaines d’ultra-pauvres.

Me, showing off with my monster stack on the final table.

Je vais rester sur 50 joueurs maximum parce que ça représente quelque chose pour lequel le calcul ICM classique est incapable de finir dans un temps raisonnable, et Monte-Carlo a du mal à être super rapide mais peut quand même me fournir des valeurs. Pour les prix (le prizepool, les payouts), on va copier sur un tournoi d’une cinquantaine de joueurs que j’ai trouvé sur Winamax au pif. Car oui, on va fixer le prizepool, je ne vois pas pourquoi on se mettrait des bâtons dans les roues, puisqu’on va par contre faire varier à fond la distribution des stacks. L’idée est de correspondre au cas d’usage pour lequel on fait tourner plein de simulations de tournoi sur une configuration donnée : 50 joueurs et prizepool déterminé.

Étape #1 : Générer les données

Pour entraîner mon réseau je vais avoir besoin de couples (input, output) = (distribution de stacks, icm). Je sais calculer l’ICM, j’ai donc juste besoin de listes de stacks variées. Comme je vais avoir du mal à extraire ces données de leurs milieux naturels (les plateformes de poker en ligne), je vais les générer en mimant les processus de mère Nature, c’est à dire en organisant des petits simili-tournois. Ca tombe bien, j’en aurai besoin plus tard pour évaluer des concurrents à l’ICM !

La conception de ces tournois est un large sujet, mais ce qui va compter ici c’est surtout de générer une variété de situations assez grande. J’ai donc pris un petit test avec des joueurs omniscients que j’ai codé et dont on va ignorer les défauts pour le moment :

• pour chaque main on va tirer un certain nombre de couples de joueurs qui vont s’affronter
• à chaque affrontement, une équité va être tirée qui va donner la probabilité que le premier joueur gagne au showdown (si les joueurs payent les relances des adversaires)
• les jeu est un simple push/call/fold : le premier joueur peut se coucher et perd sa blinde, ou relancer à tapis. S’il relance, le second joueur peut suivre et aller au showdown ou se coucher et perdre sa blinde.
• les joueurs vont jouer en connaissance de leur équité. Le second joueur va d’abord décider s’il suivra au cas où le premier joueur relance, et le premier joueur sachant tout ça (son équité et la future décision du second joueur car il est omniscient), va décider de relancer ou pas.
• pour estimer les situations futures les joueurs se servent de fonctions d’EV qui pourraient être l’ICM mais seront en l’occurence une estimation proportionnelle aux jetons (Chips EV)

On fait donc prendre leurs décisions à tous les couples de joueurs en même temps, puis on résoud en faisant les tirages aléatoires nécessaires pour les affrontements et redistribuant les jetons selon les issues de toutes les mains.

On va insérer une sonde au niveau de l’évaluation d’EV pour répertorier toutes les situations qui sont évaluées dans un bon vieux Set[Tuple] histoire de ne pas avoir de doublons, et hop on peut jouer des tournois pour générer des distributions de stacks crédibles.

Aujourd’hui je ne vous colle pas le code : on est prooches de la fin de cette petite épopée, et je mettrai simplement mon code à disposition sur Github une fois que tout sera fini.

Étape #2 : Calculer l’ICM

On a joué autant de simili-tournois que nécessaire pour avoir assez (N) de situations différentes, et nous allons maintenant calculer l’ICM de chaque :

• prenons en échantillon toutes les situations générées par un tournoi supplémentaire
• observons la convergence des caculs d’ICM méthode Monte-Carlo pour récupérer le nombre de tirages nécessaires à une bonne précision probable pour chaque situation
• prenons le maximum de ces nombres, ce qui est bien pessimiste
• pour toutes les N situations générées précédemment, calculons l’ICM avec ce nombre de tirages

Grâce à notre pessimisme, on ne doit pas s’éloigner beaucoup (en fréquence et en distance) des garanties statistiques de notre échantillon et on va prendre le raccourci de considérer qu’on a les mêmes garanties.

Étape #3 : Définition du NN (Neural Network)

Comment construit-on un NN ? À tâtons. Sisi. Enfin on peut quand même trouver de bons conseils pour orienter ses tâtonnements de manière pertinente. À ce sujet et après avoir bien compris de quoi il retourne, je ne peux que vous conseiller le blog de Jason Brownlee qui couvre énormément de cas et de questions que les data scientists se posent en pratique.

Pour le détail, on va normaliser en peu nos données :

• en input on va considérer uniquement des stacks triés par ordre décroissants (on a fait ça au moment même de la génération des stacks et avant de calculer l’ICM) et divisés par la somme des stacks
• en output on va diviser l’ICM par la somme des payouts (qui est la somme des valeurs d’ICM)

Si vous vous rappelez du calcul de l’ICM, on est dans des combinaisons de multiplications et de sommes et les couches de neurones denses - chaque neurone est connecté à chaque neurone de la couche suivante - se prêtent particulièrement bien à ce ce genre de calculs. Après quelques essais, j’ai trouvé que cette forme de réseau marchait pas mal :

         [Input layer] : nb_players neurons (stacks)
        | | | | | | | | | | | | | | | | | | | | | |
         [Hidden layer 1] : 3 * nb_players neurons
        | | | | | | | | | | | | | | | | | | | | | |
         [Hidden layer 2] : 3 * nb_players neurons
        | | | | | | | | | | | | | | | | | | | | | |
         [Output layer] : nb_players neurons (ICM)

On utilise de traditionnelles fonctions d’activation relu, une fonction de perte mean_squared_error et un optimizer RMS ce qui correspond bien à un problème de régression.

Ça nous donne pour du Keras :

    nn = Sequential()
    nn.add(Dense(nb_players, activation='relu'))
    nn.add(Dense(nb_players * 3, activation='relu'))
    nn.add(Dense(nb_players * 3, activation='relu'))
    nn.add(Dense(nb_players, activation='relu'))
    nn.compile(
        loss='mean_squared_error',
        optimizer=keras.optimizers.RMSprop(),
        metrics=[keras.metrics.RootMeanSquaredError()]
    )

Entrainement et résultats

• 9k situations d’entraînement
• 1k situations de validation
• 1k situations de test
• une configuration de tournoi avec
  • 50 joueurs
  • 100 blindes de stack initial
  • les blindes qui sont multipliées toutes les 10 mains par 1,3
  • 30% des joueurs qui participent à chaque main (comme sur une table de 6 joueurs en gros)
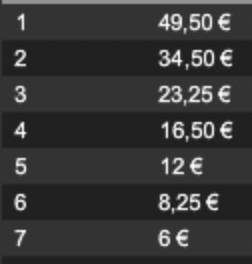
• le prizepool : 4650. 3450. 2325. 1650. 1200. 825. 600 0 0 0 ...
• donc un buy-in de 294 milliards de dollars (pourquoi pas)
• une précision pour les évaluation ICM en Monte-Carlo de un demi buy-in avec 90% de confiance

J’obtiens un nombre de tirages nécessaires pour chaque évaluation ICM de 3100.

Je fais tourner mes calculs en multithread pendant une minute environ pour une moyenne de 6ms par évaluation ICM (mais le multithread n’est pas facilement réalisable au sein d’un tournoi, on est plutôt autour de 15ms en monothread).

Maintenant que j’ai toutes mes situations et les estimations ICM associées, j’entraîne mon NN pour 10 epochs avec un batch-size de 30 - pour ceux à qui ça parle - ce qui me prend environ 5 secondes.

Un petit plot pour la convergence du NN :

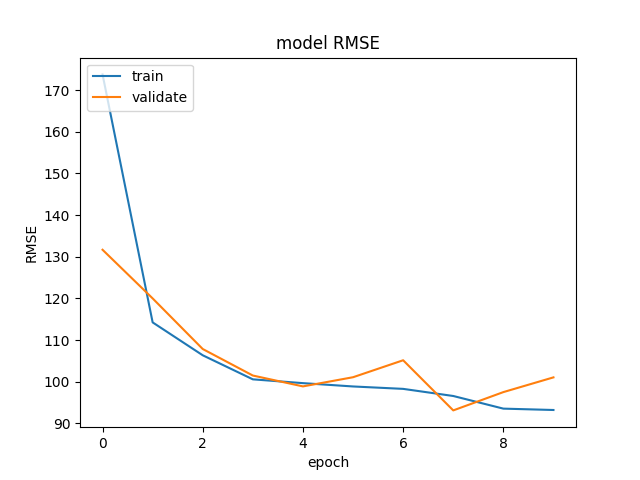
et sur les tests finaux une RMSE (root means squared error) moyenne de 100.62 (milliards de dollars).

Ce que ça veut dire, c’est qu’en une minute j’ai entraîné un réseau de neurones dont les erreurs par rapport aux évaluations de Monte-Carlo sont de l’ordre de la précision de ces évaluations. Et ça, c’est déjà pas mal !

Mais l’objectif était d’aller plus vite que les quelques millisecondes de calculs de Monte-Carlo, et ça se confirme en effet.

Temps de calcul d’une évaluation ICM en utilisant le modèle Keras : 19 microsecondes ! Objectif atteint : on a divisé par 316 le temps de calcul par rapport à l’évaluation de Monte-Carlo.

Allez, une dernière optimisation pour la route : Keras étant utilisé tant pour l’entraînement tant que l’évaluation, il est possible de dégraisser un peu tout ça en utilisant TensorFlow lite (un bon guide ici). Et dans ce cas, on obtient moins de 10 microsecondes par évaluation.

Concluons

Je vous ai caché quelques technicités, notamment l’exposition des fonctions de calcul d’ICM codées en C++ à du code Python grâce à Boost qui fut une aventure déplaisante mais relativement efficace. Ceci-dit, voilà, on peut calculer l’ICM avec une bonne précision en quelques micro-secondes moyennant une étape préliminaire d’environ une minute. On peut augmenter cette précision ce qui gonflera le temps de préparation, mais si on travaille à configuration de tournoi fixe et pour un nombre important de tournois, on passera très certainement énormément moins de temps au total.

La suite ? On va enfin faire des simulations marrantes avec de l’ICM et tenter de comprendre quels sont son domaine d’application, ses limites, et si on a le temps on cherchera à créer de meilleures évaluations.

Malgré les milliards de mails par secondes que je reçois concernant ces expériences, n’hésitez pas à m’écrire pour me dire ce que vous en pensez ou me poser toute question - ou me proposer une mission autour de l’IA ;)